La velocidad de la luz (2)

Figura 1. Diferentes histogramas con los 66 datos de Newcomb.

La primera observación evidente sobre los datos de Newcomb es que éstos varían. ¿Porqué? Se supone que, sobre todo, cada observación se hizo con el mismo patrón, medida por un observador cualificado y con el mismo aparato cada vez. Newcomb sabía, y nosotros también, que las medidas más precisas casi siempre varían. El entorno de cada medida es ligeramente diferente. El aparato cambia un poco con la temperatura, la densidad de la atmósfera también cambia de un día a otro, y así con otros detalles. Newcomb hizo lo que pudo para eliminar las fuentes de variación que podía anticipar y su experimento 0btuvo unas observaciones con menos variación que las de los científicos anteriores. Pero incluso el mejor experimento produce resultados variables. Por ello Newcomb tomó muchas medidas y no sólo una. La media de los 66 valores es menos variable que el resultado de una única medida, la media no depende tanto de la temperatura y la densidad atmosférica como una sola observación. Si nos ponemos ahora en el lugar de Newcomb, estaremos tentados por calcular la media de los datos, convertir esta velocidad en una nueva y mejor estimación de la velocidad de la luz y salir corriendo para incrementar nuestra reputación al publicar el resultado. La tentación de hacer un cálculo rutinario y anunciar la respuesta se presenta siempre que los datos han sido recogidos para contestar una cuestión específica. Las computadoras son muy buenas para los cálculos rutinarios, de manera que sucumbir a la tentación es un camino fácil. El primer paso hacia la sofisticación estadística es resistir la tentación de calcular sin pensar. Como la variabilidad está presente en cualquier conjunto de datos, debemos primero examinar la naturaleza de la variación y, en algunos casos, quedaremos sorprendidos por lo que veremos.

La distribución

El patrón de variación de una variable es su distribución. La distribución presenta los valores numéricos que toma una variable y la frecuencia con la que cada valor ocurre.

La mejor manera de observar una distribución es representarla gráficamente. Conocemos varias técnicas gráficas para representar los datos de Newcomb. En particular el histograma.

Para hacer un histograma, se procede en tres pasos:

1. Se divide el rango de los datos en clases, casi siempre de la misma longitud.
2. Se cuenta el número de observaciones que caen en cada clase, es decir, las frecuencias absolutas y se construye la tabla de frecuencias.
3. Se dibuja el histograma.

Como el propósito de un histograma es mostrar la forma de una distribución, debemos estar muy atentos a los aspectos más visuales del gráfico. Nuestros ojos responden al área de las barras, de forma que ésta ha de ser proporcional a la frecuencia de la clase.

Ahora bien, antes de dibujar un histograma hay que decidir el número de clases, y eso es cuestión de opiniones.

La figura 1 se ha creado con el siguiente código:

tiempo <- Newcomb$Time*10^9 - 24800

png("histogramas.png")
oldpar <- par(mfrow=c(2,2))

hist.a <- hist(tiempo, breaks=-60+5*1:25, main=NULL, xlab="Tiempo (a)", ylab="Frecuencia", ylim=c(0,30), col="grey")
text(hist.a$mids, hist.a$counts, labels=ifelse(hist.a$counts==0,"",hist.a$counts), pos=3)

hist.b <- hist(tiempo, breaks=-52.5+5*1:25, main=NULL, xlab="Tiempo (b)", ylab="Frecuencia", ylim=c(0,30), col="grey")
text(hist.b$mids, hist.b$counts, labels=ifelse(hist.b$counts==0,"",hist.b$counts), pos=3)

hist.c <- hist(tiempo, breaks=c(-44,-33.5,-23,-12.5,-2,8.5,19,29.5,40,50.5), 
                          main=NULL, xlab="Tiempo (c)", ylab="Frecuencia", ylim=c(0,45), col="grey")
text(hist.c$mids, hist.c$counts, labels=ifelse(hist.c$counts==0,"",hist.c$counts), pos=3)

hist.d <- hist(tiempo, breaks=-60+10*1:12, main=NULL, xlab="Tiempo (d)", ylab="Frecuencia", ylim=c(0,45), col="grey")
text(hist.d$mids, hist.d$counts, labels=ifelse(hist.d$counts==0,"",hist.d$counts), pos=3)

par(oldpar)
dev.off()

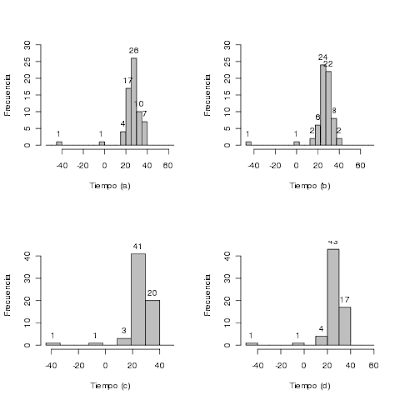
Los histogramas de la figura 1 son diferentes en función de les clases que formemos.

1. En el caso (a) el histograma está formado con los intervalos ]-60,-55], ]-55,-50],... de anchura 5 y marca de clase en los puntos –57.5, -52.5,..., -2.5, 2.5,..., 52.5, 57.5.
2. En (b) el histograma está formado con los intervalos ]-52.5,-47.5], ]-47.5,-42.5],..., también con una longitud de 5 y con las marcas de clase en los valores -50, -45,..., -5, 0, 5,...,60.
3. Si nosotros no decidimos los límites de los intervalos, la macro de Excel “Análisis de datos:Histograma” proporciona el gráfico (c). La anchura de los intervalos es 10.5 y el límite inferior del primer intervalo es el valor mínimo –44. El programa de Estadística SPSS construye un histograma con las marcas de clase -40, -30,..., -10, 0, 10,..., 40 y, por tanto, intervalos de longitud 10.
4. Cuando consideramos intervalos de anchura 10 y centrados con marcas de clase -55, -45,..., -5, 5,..., 55, tenemos el histograma (d).

Los histogramas anteriores tienen la característica común de que todos los intervalos son de la misma longitud. Con estos datos podríamos considerar un primer intervalo, como por ejemplo ]-45,-15] que tiene una frecuencia absoluta de 2, y dibujar una barra con la altura de manera que el área sea proporcional a 2.

hist.e <- hist(tiempo, breaks=c(-45,15,20,25,30,35,40), 
                       main=NULL, xlab="Tiempo (e)", 
                       ylab="Frecuencia", ylim=c(0,0.09), col="grey")
text(hist.e$mids, hist.e$intensities,
                  labels=ifelse(hist.e$counts==0,"",hist.e$counts), pos=3)
lines(density(tiempo))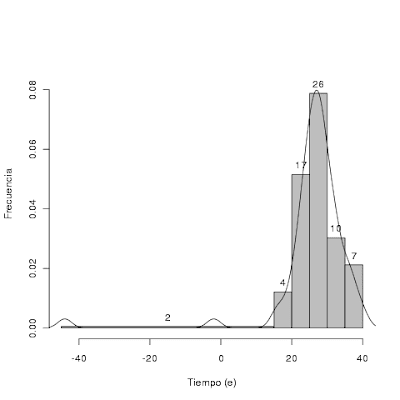 

Otro tipo de gráfico que podemos utilizar con estos datos es el gráfico de tallo y hojas (stem and leaf):

stem(tiempo)

El resultado es, más o menos, así:

## 
##   The decimal point is 1 digit(s) to the right of the |
## 
##   -4 | 4
##   -3 | 
##   -2 | 
##   -1 | 
##   -0 | 2
##    0 | 
##    1 | 669
##    2 | 01122333444445555566666777777888888899999
##    3 | 0001122222334666679
##    4 | 0

La construcción de este gráfico no es tan arbitraria como el histograma y permite la reproducción de los datos originales.

Cualquier científico de laboratorio sabe que incluso las medidas más precisas varían, pero espera una distribución simétrica y con un único pico. Entonces el mejor estimador del verdadero valor de la cantidad medida es el centro de la distribución. Los histogramas y el gráfico de tallo y hojas muestran que Newcomb no fue afortunado, ya que los datos contienen valores atípicos (outliers). ¿Qué hay que hacer con ellos?

(continuará...)